When Is Electric Potential Zero

Line integral of the electric field

Electric potential
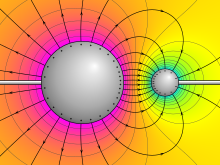Electric potential around two oppositely charged conducting spheres. Purple represents the highest potential, yellow zero, and cyan the lowest potential. The electric field lines are shown leaving perpendicularly to the surface of each sphere.
Mutual symbols	V, φ
SI unit	volt
Other units	statvolt
In SI base of operations units	Five = kg⋅mⁱⁱ⋅s⁻ⁱⁱⁱ⋅A⁻¹
Extensive?	yes
Dimension	One thousand 50 ⁱⁱ T ⁻³ I ⁻¹

The electric potential (as well called the electric field potential, potential driblet, the electrostatic potential) is defined every bit the corporeality of work free energy needed to move a unit of measurement of electric charge from a reference indicate to the specific point in an electrical field. More precisely, it is the energy per unit accuse for a test charge that is so small that the disturbance of the field under consideration is negligible. Furthermore, the motion across the field is supposed to proceed with negligible acceleration, and so every bit to avoid the test accuse acquiring kinetic free energy or producing radiation. By definition, the electrical potential at the reference betoken is zero units. Typically, the reference point is globe or a point at infinity, although any bespeak can be used.

In classical electrostatics, the electrostatic field is a vector quantity expressed equally the gradient of the electrostatic potential, which is a scalar quantity denoted by $5$ or occasionally $φ$ ,^[1] equal to the electrical potential free energy of any charged particle at any location (measured in joules) divided by the accuse of that particle (measured in coulombs). By dividing out the charge on the particle a quotient is obtained that is a holding of the electric field itself. In curt, an electric potential is the electric potential energy per unit charge.

This value can be calculated in either a static (fourth dimension-invariant) or a dynamic (time-varying) electric field at a specific time with the unit joules per coulomb (J⋅C⁻¹) or volt (V). The electric potential at infinity is assumed to be zero.

In electrodynamics, when time-varying fields are nowadays, the electric field cannot be expressed only in terms of a scalar potential. Instead, the electric field can be expressed in terms of both the scalar electrical potential and the magnetic vector potential.^[two] The electric potential and the magnetic vector potential together form a 4-vector, so that the two kinds of potential are mixed under Lorentz transformations.

Practically, the electrical potential is a continuous function in all space, because a spatial derivative of a discontinuous electrical potential yields an electric field of impossibly infinite magnitude. Notably, the electric potential due to an idealized indicate charge (proportional to $1 ⁄ r$ , with $r$ the distance from the signal charge) is continuous in all space except at the location of the point charge. Though electric field is not continuous across an idealized surface charge, it is non infinite at any point. Therefore, the electric potential is continuous across an idealized surface charge. Additionally, an idealized line of charge has electric potential (proportional to $ln(r)$ , with $r$ the radial distance from the line of charge) is continuous everywhere except on the line of accuse.

Introduction [edit]

Classical mechanics explores concepts such as force, energy, and potential.^[three] Force and potential free energy are directly related. A net force acting on any object will crusade it to accelerate. As an object moves in the direction of a force acting on information technology, its potential energy decreases. For example, the gravitational potential energy of a missive at the tiptop of a hill is greater than at the base of the hill. As it rolls downhill, its potential energy decreases and is being translated to motion – kinetic energy.

It is possible to define the potential of certain force fields so that the potential energy of an object in that field depends simply on the position of the object with respect to the field. Two such strength fields are a gravitational field and an electric field (in the absence of time-varying magnetic fields). Such fields touch on objects because of the intrinsic backdrop (e.g., mass or charge) and positions of the objects.

An object may possess a property known equally electric charge. Since an electric field exerts force on a charged object, if the object has a positive charge, the force will be in the direction of the electrical field vector at the location of the charge; if the charge is negative, the force will be in the opposite direction.

The magnitude of strength is given past the quantity of the charge multiplied by the magnitude of the electric field vector,

|\mathbf {F} |=q|\mathbf {E} |.

Electrostatics [edit]

Electric potential of split up positive and negative indicate charges shown as color range from magenta (+), through yellow (0), to cyan (−). Circular contours are equipotential lines. Electric field lines leave the positive charge and enter the negative accuse.

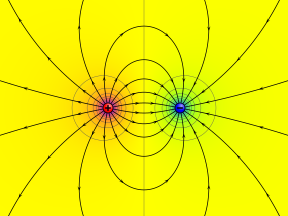
Electric potential in the vicinity of two opposite betoken charges.

The electrical potential at a bespeak $r$ in a static electrical field $E$ is given by the line integral

$V_{\mathbf {E} }=-\int _{\mathcal {C}}\mathbf {E} \cdot \mathrm {d} {\boldsymbol {\ell }}\,$

where $C$ is an arbitrary path from some stock-still reference point to $r$ . In electrostatics, the Maxwell-Faraday equation reveals that the ringlet ${\textstyle \nabla \times \mathbf {Eastward} }$ is zero, making the electric field conservative. Thus, the line integral above does not depend on the specific path $C$ chosen simply only on its endpoints, making ${\textstyle V_{\mathbf {E} }}$ well-defined everywhere. The gradient theorem then allows us to write:

$\mathbf {E} =-\mathbf {\nabla } V_{\mathbf {Eastward} }\,$

This states that the electric field points "downhill" towards lower voltages. Past Gauss's law, the potential can likewise be plant to satisfy Poisson's equation:

\mathbf {\nabla } \cdot \mathbf {E} =\mathbf {\nabla } \cdot \left(-\mathbf {\nabla } V_{\mathbf {East} }\right)=-\nabla ^{ii}V_{\mathbf {E} }=\rho /\varepsilon _{0}

where $ρ$ is the total charge density and ${\textstyle \mathbf {\nabla } \cdot }$ denotes the deviation.

The concept of electrical potential is closely linked with potential energy. A examination charge, $q$ , has an electric potential energy, $U E$ , given by

U_{\mathbf {E} }=q\,V.

The potential energy and hence, also the electric potential, is only defined upwardly to an condiment constant: i must arbitrarily choose a position where the potential free energy and the electric potential are zero.

These equations cannot exist used if ${\textstyle \nabla \times \mathbf {E} \neq \mathbf {0} }$ , i.east., in the case of a non-bourgeois electric field (caused by a changing magnetic field; encounter Maxwell's equations). The generalization of electric potential to this case is described in the section § Generalization to electrodynamics.

Electric potential due to a point charge [edit]

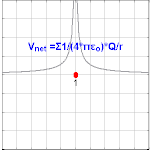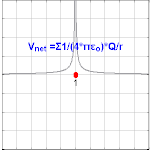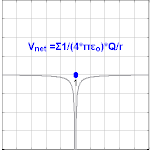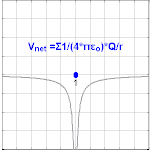
The electrical potential created past a charge, Q, is V =Q/(4πε₀ r). Different values of Q yield different values of electric potential, V, (shown in the prototype).

The electric potential arising from a betoken charge, $Q$ , at a distance, $r$ , from the location of $Q$ is observed to be

V_{\mathbf {E} }={\frac {1}{4\pi \varepsilon _{0}}}{\frac {Q}{r}},

where $ε 0$ is the permittivity of vacuum^[4], $Five East$ is known as the Coulomb potential, and the ratio,

k_{e}={\frac {1}{4\pi \varepsilon _{0}}}

is known equally the Coulomb constant.

The electric potential at whatever location, ${\textstyle {\textbf {r}}}$ , in a system of betoken charges is equal to the sum of the private electric potentials due to every signal charge in the system. This fact simplifies calculations significantly, because addition of potential (scalar) fields is much easier than add-on of the electric (vector) fields. Specifically, the potential of a ready of discrete point charges $q i$ at points $r i$ becomes

V_{\mathbf {E} }(\mathbf {r} )=k_{e}\sum _{i}{\frac {q_{i}}{|\mathbf {r} -\mathbf {r} _{i}|}},

where

and the potential of a continuous charge distribution $ρ (r)$ becomes

V_{\mathbf {E} }(\mathbf {r} )=k_{due east}\int _{R}{\frac {\rho (\mathbf {r} ')}{|\mathbf {r} -\mathbf {r} '|}}d^{3}r'.

Where

The equations given above for the electrical potential (and all the equations used here) are in the forms required by SI units. In some other (less common) systems of units, such equally CGS-Gaussian, many of these equations would be altered.

Generalization to electrodynamics [edit]

When fourth dimension-varying magnetic fields are present (which is true whenever there are time-varying electric fields and vice versa), information technology is non possible to depict the electric field merely in terms of a scalar potential $V$ because the electric field is no longer conservative: $\textstyle \int _{C}\mathbf {Due east} \cdot \mathrm {d} {\boldsymbol {\ell }}$ is path-dependent because $\mathbf {\nabla } \times \mathbf {East} \neq \mathbf {0}$ (due to the Maxwell-Faraday equation).

Instead, 1 can still define a scalar potential by also including the magnetic vector potential $A$ . In detail, $A$ is defined to satisfy:

\mathbf {B} =\mathbf {\nabla } \times \mathbf {A}

where $B$ is the magnetic field. By the cardinal theorem of vector calculus, such an $A$ tin always exist found, since the deviation of the magnetic field is always zero due to the absence of magnetic monopoles. Now, the quantity

\mathbf {F} =\mathbf {E} +{\frac {\fractional \mathbf {A} }{\fractional t}}

is a conservative field, since the roll of $\mathbf {East}$ is canceled past the curl of ${\frac {\partial \mathbf {A} }{\partial t}}$ according to the Maxwell–Faraday equation. One can therefore write

\mathbf {Eastward} =-\mathbf {\nabla } V-{\frac {\partial \mathbf {A} }{\partial t}},

where $5$ is the scalar potential divers by the bourgeois field $F$ .

The electrostatic potential is simply the special case of this definition where $A$ is time-invariant. On the other manus, for time-varying fields,

-\int _{a}^{b}\mathbf {Eastward} \cdot \mathrm {d} {\boldsymbol {\ell }}\neq V_{(b)}-V_{(a)}

unlike electrostatics.

Estimate freedom [edit]

The electrostatic potential could have any constant added to it without affecting the electric field. In electrodynamics, the electric potential has infinitely many degrees of liberty. For whatever (perhaps fourth dimension-varying or space-varying) scalar field, $\psi$ , we tin can perform the following guess transformation to discover a new ready of potentials that produce exactly the same electric and magnetic fields:^[5]

V^{\prime number }=5-{\frac {\partial \psi }{\fractional t}}

\mathbf {A} ^{\prime }=\mathbf {A} +\nabla \psi

Given unlike choices of gauge, the electric potential could take quite different properties. In the Coulomb gauge, the electric potential is given past Poisson's equation

\nabla ^{2}V=-{\frac {\rho }{\varepsilon _{0}}}

just like in electrostatics. However, in the Lorenz gauge, the electric potential is a retarded potential that propagates at the speed of lite and is the solution to an inhomogeneous moving ridge equation:

\nabla ^{2}5-{\frac {1}{c^{2}}}{\frac {\partial ^{2}V}{\partial t^{2}}}=-{\frac {\rho }{\varepsilon _{0}}}

Units [edit]

The SI derived unit of electric potential is the volt (in accolade of Alessandro Volta), denoted as V, which is why the electric potential deviation between two points in space is known as a voltage. Older units are rarely used today. Variants of the centimetre–gram–2d organisation of units included a number of different units for electric potential, including the abvolt and the statvolt.

Galvani potential versus electrochemical potential [edit]

Inside metals (and other solids and liquids), the energy of an electron is afflicted not only by the electric potential, but also by the specific atomic surroundings that it is in. When a voltmeter is continued between two dissimilar types of metallic, it measures the potential difference corrected for the different atomic environments.^[6] The quantity measured by a voltmeter is called electrochemical potential or fermi level, while the pure unadjusted electrical potential, $V$ , is sometimes chosen the Galvani potential, $\phi$ . The terms "voltage" and "electric potential" are a bit ambiguous but i may refer to either of these in unlike contexts.

Encounter also [edit]

Absolute electrode potential
Electrochemical potential
Electrode potential

References [edit]

^ Goldstein, Herbert (June 1959). Classical Mechanics. U.s.: Addison-Wesley. p. 383. ISBN0201025108.
^ Griffiths, David J. (1999). Introduction to Electrodynamics. Pearson Prentice Hall. pp. 416–417. ISBN978-81-203-1601-0.
^ Young, Hugh A.; Freedman, Roger D. (2012). Sears and Zemansky's University Physics with Modern Physics (13th ed.). Boston: Addison-Wesley. p. 754.
^ "2018 CODATA Value: vacuum electric permittivity". The NIST Reference on Constants, Units, and Doubt. NIST. 20 May 2019. Retrieved 2019-05-twenty .
^ Griffiths, David J. (1999). Introduction to Electrodynamics (third ed.). Prentice Hall. p. 420. ISBN013805326X.
^ Bagotskii VS (2006). Fundamentals of electrochemistry. p. 22. ISBN978-0-471-70058-6.